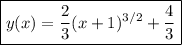The left side is the derivative of
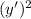 :
:

So we can integrate both sides of
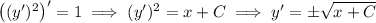
Then integrate again to solve for
 :
:
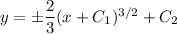
With the given initial conditions, we find
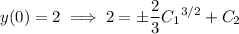
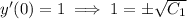
The second equation says
 is either 1 or -1, but in the latter case, we would get
is either 1 or -1, but in the latter case, we would get
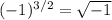 in the first equation, which is undefined over the real numbers, so
in the first equation, which is undefined over the real numbers, so
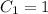 .
.
So there are two candidate solutions,
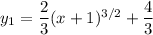
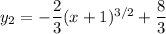
However, the second equation doesn't satisfy the initial value of the derivative, since
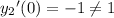 . So the solution is
. So the solution is