Question

Tarzan has foolishly gotten himself into another scrape with the animals and must be rescued once again by Jane. The 60.0 kg Jane starts from rest at a height of 5.50 m in the trees and swings down to the ground using a thin, but very rigid, 32.0 kg vine 8.50 m long. She arrives just in time to snatch the 72.0 kg Tarzan from the jaws of an angry hippopotamus. What is Jane's (and the vine's) angular speed

Answer 1

Complete part of Question: What is Jane's (and the vine's) angular speed just before she grabs Tarzan

Answer:

Jane's (and the vine's) angular speed just before she grabs Tarzan, w = 1.267 rad/s

Step-by-step explanation:

According to the law of energy conservation:

Total change in kinetic energy = Total change in potential energy

Mass of Jane = 60 kg

Mass of the vine = 32 kg

Mass of Tarzan = 72 kg

Height of Tarzan = 5.50 m

Length of the vine = 8.50 m

Jane's change in gravitational potential energy,

`U_J = 60 * 9.8 * 5.5\\U_J = 3234 J`

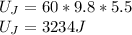
Vine's gravitational potential energy,

`U_v = Mgh/2\\U_v = 32*9.8*5.5/2\\U_v = 862.4J`

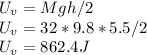
Vine's Kinetic energy :

`KE_V = 0.5 I w^(2) \\I_V = (ML^2)/(3) = (32 * 8.5^2)/(3) = 770.67 kg m^2\\ KE_V = 0.5 *770.67 * w^(2)\\KE_V = 385.33 w^(2)`

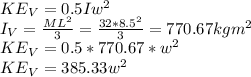
Jane's Kinetic energy:

`KE_J = 0.5m(wL)^2\\KE_J = 0.5*60(w * 8.5)^2\\KE_J = 2167.5 w^2`

`U_J + U_V = KE_J + KE_V`

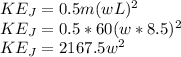
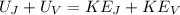
3234 + 862.4 = 2167.5w² + 385.33w²

4096.4 = 2552.83w²

w² = 4096.4/2552.83

w² = 1.605

w = √1.605

w = 1.267 rad/s