Answer:
We conclude that there is no significant difference in the proportion of all Illinois high school freshmen and seniors who have used anabolic steroids.
Step-by-step explanation:
We are given that a study by the National Athletic Trainers Association surveyed random samples of 1679 high school freshmen and 1366 high school seniors in Illinois.
Results showed that 34 of the freshmen and 24 of the seniors had used anabolic steroids.
Let
 = proportion of Illinois high school freshmen who have used anabolic steroids.
= proportion of Illinois high school freshmen who have used anabolic steroids.
 = proportion of Illinois high school seniors who have used anabolic steroids.
= proportion of Illinois high school seniors who have used anabolic steroids.
SO, Null Hypothesis,
 :
:
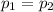 {means that there is no significant difference in the proportion of all Illinois high school freshmen and seniors who have used anabolic steroids}
{means that there is no significant difference in the proportion of all Illinois high school freshmen and seniors who have used anabolic steroids}
Alternate Hypothesis,
 :
:
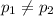 {means that there is a significant difference in the proportion of all Illinois high school freshmen and seniors who have used anabolic steroids}
{means that there is a significant difference in the proportion of all Illinois high school freshmen and seniors who have used anabolic steroids}
The test statistics that would be used here Two-sample z test for proportions;
T.S. =
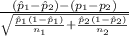 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of high school freshmen who have used anabolic steroids =
= sample proportion of high school freshmen who have used anabolic steroids =
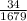 = 0.0203
= 0.0203
 = sample proportion of high school seniors who have used anabolic steroids =
= sample proportion of high school seniors who have used anabolic steroids =
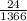 = 0.0176
= 0.0176
 = sample of high school freshmen = 1679
= sample of high school freshmen = 1679
 = sample of high school seniors = 1366
= sample of high school seniors = 1366
So, the test statistics =
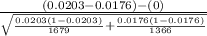
= 0.545
The value of z test statistics is 0.545.
Since, in the question we are not given with the level of significance so we assume it to be 5%. Now, at 5% significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.
Since our test statistic lies within the range of critical values of z, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.
Therefore, we conclude that there is no significant difference in the proportion of all Illinois high school freshmen and seniors who have used anabolic steroids.