Question

The potential in a region between x = 0 and x = 6.00 m is V = a + bx, where a = 10.6 V and b = -4.90 V/m. (a) Determine the potential at x = 0. 10.6 V Determine the potential at x = 3.00 m. V (b) Determine the magnitude and direction of the electric field at x = 0. magnitude V/m direction Determine the magnitude and direction of the electric field at x = 3.00 m. magnitude V/m direction

Answer 1

The electric potential at x = 0 is 10.6 V, and at x = 3.00 m it is -4.1 V. The magnitude of the electric field is 4.90 V/m for any value of x, and its direction is in the negative x-direction.

Step-by-step explanation:

The electric potential at a point in space is the amount of electric potential energy that a unit electric charge would have at that point. Given the potential function V = a + bx, where a = 10.6 V and b = -4.90 V/m, we can determine the potential at specific points as well as the electric field.

(a) At x = 0, the potential V = a + b(0) = 10.6 V + (-4.90 V/m)(0) = 10.6 V. At x = 3.00 m, the potential V = a + bx = 10.6 V + (-4.90 V/m)(3.00 m) = 10.6 V - 14.7 V = -4.1 V.

(b) The magnitude of the electric field can be determined by the negative derivative of the potential function with respect to x, which gives E = -dV/dx = -b. At x = 0 or any other point, since b is a constant, the magnitude of the electric field E = |-b| = |-(-4.90 V/m)| = 4.90 V/m. The direction of the electric field is opposite the direction in which the potential increases, which in this case is in the negative x-direction.

Answer 2

a)

When x = 0 m, V = 10.6 - 4.90*(0) = 10.6 V

When x = 10 m, V = 10.6 - 4.90*(10) = -38.4 V

When x = 6 m, V = 10.6 - 4.90*(6) = -18.8 V

When x = 3.00 m, V = 10.6 - 4.90*(3.00) = -4.1 V

b)
`E=4.90 V/m`

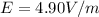
Step-by-step explanation:

a) If V = a + bx , and a = 10.6 V and b = -4.90 V/m we have:

`V=10.6-4.90x`

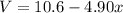
When x = 0 m, V = 10.6 - 4.90*(0) = 10.6 V

When x = 10 m, V = 10.6 - 4.90*(10) = -38.4 V

When x = 6 m, V = 10.6 - 4.90*(6) = -18.8 V

When x = 3.00 m, V = 10.6 - 4.90*(3.00) = -4.1 V

b) The electric field is:

`E=-(dV)/(dx)`

`E=-b`

`E=4.90 V/m`

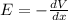
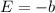
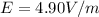
In this particular case E depends only of b, it means E is a constant value. Therefore, E = 4.9 V/m when x = 0 m and when x = 3.00 m.

I hope it helps you!