Let d represent one side distance and t represent time.
We have been given that Margret drove to a business appointment at 70 mph.
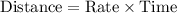
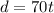
We are also told that her average speed on the return trip was 60 mph. Her return trip took her one third of an hour longer because of heavy traffic.
We can represent this information in an equation as:
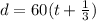
Now we will equate both distances and solve for t as:

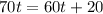

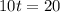
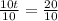
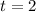
Upon substituting
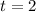 in equation
in equation
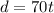 , we will get:
, we will get:
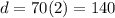
Therefore, Margret traveled 140 miles to her appointment.