Question

The probability that a person in the United States has type A positive blood is 31%. Three unrelated people in the United states are selected at random. Find the following probabilities. Round your answers to the thousandths place. A) Find the probability that all three have type A positive blood. B) Find the probability that none of the three have A positive blood. C) Find the probability that at least one of the three have A positive blood. D) Which of the events above can be considered unusual? Explain your reasoning.

Answer 1

(A) Probability that all three have type A positive blood is 0.0298.

(B) Probability that none of the three have type A positive blood is 0.3285.

(C) Probability that at least one of the three have A positive blood is 0.6715.

(D) The events which can be considered unusual is of the first part (A).

Explanation:

We are given that the probability that a person in the United States has type A positive blood is 31%.

Three unrelated people in the United states are selected at random.

The above situation can be represented through binomial distribution;

`P(X = r) = \binom{n}{r} * p^(r) * (1-p)^(n-r) ; x = 0,1,2,3,.....`

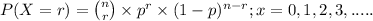
where, n = number of trials (samples) taken = 3 people

r = number of success

p = probability of success which in our question is probability that

a person in the United States has type A positive blood, i.e; 31%

Let X = Number of people in the United States has type A positive blood

So, X ~ Binom(n = 3, p = 0.31)

(A) Probability that all three have type A positive blood is given by = P(X = 3)

P(X = 3) =
`\binom{3}{3} * 0.31^(3) * (1-0.31)^(3-3)`

=
`1 * 0.31^(3) * 0.69^(0)`

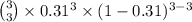
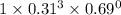
= 0.0298

(B) Probability that none of the three have type A positive blood is given by = P(X = 0)

P(X = 0) =
`\binom{3}{0} * 0.31^(0) * (1-0.31)^(3-0)`

=
`1 * 1* 0.69^(3)`

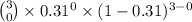
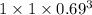
= 0.3285

(C) Probability that at least one of the three have A positive blood is given by = P(X
`\geq` 1)

P(X
`\geq` 1) = 1 - P(X = 0)

= 1 - 0.3285

= 0.6715

(D) The events above which can be considered unusual is of the first part (A) whose probability is less than 5% because an event is considered unusual whose probability is less than 5%.

Since, the probability of all three people having type A positive blood is 2.98%, so this event is considered to be unusual.