Question

The function g(x) = x2 is transformed to obtain function h:

h(x) = g(x + 7).
Which statement describes how the graph of his different from the graph of g?
O A.
The graph of h is the graph of g vertically shifted up 7 units.
B.
The graph of his the graph of g horizontally shifted left 7 units.
C.
The graph of h is the graph of g vertically shifted down 7 units.
OD.
The graph of h is the graph of g horizontally shifted right 7 units.

Answer 1

The function g(x) = x2 is transformed to obtain function h:
h(x) = g(x + 7).
Which statement describes how the graph of his different from the graph of g?
O A.
The graph of h is the graph of g vertically shifted up 7 units.

Answer 2

"The graph of his the graph of g horizontally shifted left 7 units." Which is option "B" n the list

Explanation:

If the function
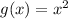`g(x)=x^2` is transformed to obtain the function
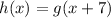`h(x)=g(x+7)`, then a transformation that affects the x-variable has taken place.

Recall that a transformation that adds t units to the variable "x" represent graphically the horizontal displacement of the original function,"t" units to the left.

Therefore, the correct answer is:

"The graph of his the graph of g horizontally shifted left 7 units."

which agrees with option "B" in your given list.