Question

The circumference of a circle is 12π m. What is the area, in square meters? Express your answer in terms of π.

Answer 1

π 36 m^2

Explanation:

C = 2π R = 12π m --> R = 6m

A = π R^2 = π 36 m^2

Answer 2

• Area of circle = 36π m²

Explanation:

In the question we are given that circumference of circle is 12π m . And we are asked to find the area of circle in term of π .

Solution : -

For finding area of circle we need to find the radius of circle . In the question circumference of circle is given . So we can find radius of circle using it . We know that ,

`\qquad \quad \pink{\underline{\pink{\boxed{\frak{Circumference_ {(Circle) }= 2\pi r}}}}}`

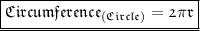
Where ,

• π refers to 3.14 or 22/7

• r refers to radius of circle

But as in the question , it is given that we have to find the area in term of π. So we aren't using π as 3.14 or 22/7 .

Now, Radius :

`\longrightarrow \qquad \: 12 \cancel{\pi }= 2 \cancel{\pi} r`

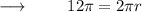
Step 1 : Cancelling π and we get :

`\longrightarrow \qquad \:12 = 2r`

Step 2 : Dividing both sides by 2 :

`\longrightarrow \qquad \: \cancel{(12)/(2) } = \frac{ \cancel{2}r}{ \cancel2}`

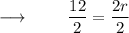
On further calculations we get :

`\longrightarrow \qquad \: \boxed{ \bf{r = 6 \: m}}`

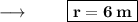
• Therefore , radius of circle is 6 m .

Finding Area :

As we have find the radius of circle above so we can find its area easily . We know that ,

`\qquad \: \qquad \pink{\underline{\pink{ \boxed{{\frak{ Area_((Circle)) = \: \pi r {}^(2) }}}}}}`

Now substituting value of radius :

`\longmapsto \: \qquad \quad\pi (6) {}^(2)`

`\longmapsto \: \qquad \quad \pi * \: 6 * 6`

`\longmapsto \: \qquad \quad \pi * 36`

We get :

`\longmapsto \: \qquad \quad \blue{\underline{\blue{\boxed{\frak{ \bf{36 \pi \: m {}^(2) }}}}}}`

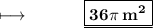
• Therefore, area of circle is 36π square metres .

#Keep Learning