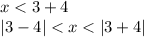Question

What is the Compound Inequality that is true for the missing side length? 3cm, 4cm, Xcm

Answer 1

`x< 3+4\: and\\\left | 3-4 \right |<x<\left | 3+4 \right |`

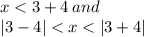
Explanation:

1. Well, when it comes to triangles. Mainly Pythagorean Triple, right triangles whose sides are 3,4,5 or 5,11,12

2. Keeping in mind this a Pythagorean Triple, then x=5

3. Then we can write it as Compound Inequality by combining the Statements for an Inequality of Triangle:

We can write it as

`5<3+4\\\left | 4-3 \right |<5<\left | 4+3 \right |`

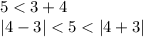
Or we can do:

`4<3+5\\\left | 4-5 \right |<4<\left | 4+5 \right |`

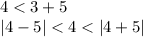
and:

`3<4+5\\\left | 4-5 \right |<3<\left | 4+5 \right |`

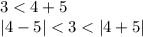
4. Writing in terms of x:

`x<3+4\\\left | 3-4 \right |<x<\left | 3+4 \right |`