Answer:
C. 210 square centimeters.
Explanation:
The figure is attached.
Notice that the whole surface area is formed by 1 square, 2 different rectangles and 2 conguent triangles. Let's find the area of each figure.
Square area:
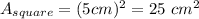
Rectangles:
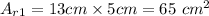
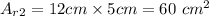
So, all rectangles have a total surface area of
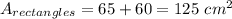
Triangles:
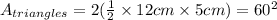
Because, there are two congruent triangle.
Now, we need to sum all areas:
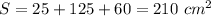
Therefore, the total surface area is 210 square centimeters. So, the right answer is C.