Question

When ø=5pi/3, what are the reference angle and the sign values for sine, cosine, and tangent? (2

When

points)

O'= 3, cosine is positive, sine and tangent are negative

57

O' = 3, sine and cosine are positive, tangent is negative

O'=

TT

3, sine and cosine are positive, tangent is negative

-

O'=

St

3, cosine is positive, sine and tangent are negative

Answer 1

The reference angle is
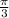`(\pi)/(3)`. Sine:negative, Cosine:positive, Tangent:Negative

Explanation:

Given an angle that is in the range
`[0,2\pi]`, you must apply the following:

1. If the angle is in the first quadrant, then the reference angle is the same.

2. If the angle is in the second quadrant, then the reference angle is
`180-\theta`

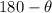
3. If the angle is in the third quadrant, then the reference angle is
`\theta-180`

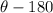
4. If the angle is in the fourth quadrant, then the reference angle is
`360-\theta`

We are given that
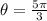`\theta = (5 \pi)/(3)`. This angle is in the range
`[0,2\pi]`, and this angle is in the fourth quadrant. Recall that 360° are equivalent to
`2\pi` radians.

So the reference angle is

`2\pi - (5\pi)/(3) = (\pi)/(3)`.

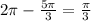The sign of the sine of this angle is determined of the sign of the y coordinate of one number of the same quadrant. Take for example the number (1,-1). This means that sine has a negative sign. To check the cosine sign, we check the sign of the x coordinate of (1,-1). Since it is positive, the cosine is positive.

Since tangent = sine/cosine and taking into account the law of signs, we have that tangent has a negative sign in this quadrant.

Answer 2

the reference angle is given by
`(\pi)/(3)`

sine = negative

cosine = positive

tangent = negative

Explanation:

We have been given the angle
`\theta=(5\pi)/(3)`

The angle lies in Quadrant IV. Hence, in order to find the reference angle, we can subtract this angle with
`2\pi`

Therefore, the reference angle is given by

`2\pi - (5\pi)/(3) \\\\=(\pi)/(3)`

In Quadrant IV, cosine and secant functions are positive and rest trigonometric functions are negative.

Thus, we have

sine = negative

cosine = positive

tangent = negative