Answer:
(D)
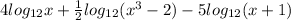
4 log Subscript 12 Baseline x + one-half log Subscript 12 Baseline (x cubed minus 2) minus 5 log Subscript 12 Baseline (x + 1)
Explanation:
Given the expression:
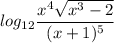
We first apply the division law of logarithm:
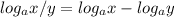
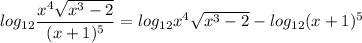
Next, by addition law:
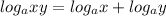
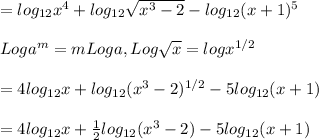
The correct option is D.