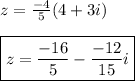Question

In an Argand diagram, the point P represents the complex number z, where z = x + iy. Given that z + 2 = λi(z + 8), where λ is a real parameter, find the Cartesian equation of the locus of P as λ varies. If also z = μ(4 + 3i), where λ is real, prove that there is only one possible position for P

Answer 1

The answer is "
`\boxed{z= (-16)/(5)- (-12)/(15)i}`".

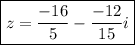Step-by-step explanation:

As the problem stands

At the point of P, it is the complex number z in the Diagram of Argand and z = X+iy.

We have said this:
`(z+2)= \lambda i (z +8) .... (i)`

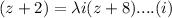
where the
`\lambda` parameter is a true

The conceptual equation of the locus P varies between
`z = x+iy \ \ \ to \ \ \ \lambda`

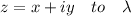
And in equation mentioned above.

`x+iy+2=\lambda i(x+iy+8) \\\\x+iy+2= \lambda xi+ \lambda i^2y+\lambda 8i\\\\ x+2+iy=-y \lambda +i(x+8)\lambda\\\ compare \ real \ and \ imaginary\ part \\\\\ x+2 = -y\lambda \\\\y= (x+8) \lambda\\\\ \lambda = (x+2)/(-y) \\ \\ \lambda = (y)/(x+8)`

`y^2= -x^2-10x-16 ....(ii)\\\\z= \mu (4+3i)....(iii)\\\\\ z= x+iy \\\\x+iy = 4\mu + 3 \mu i \\\\x= 4\mu \\\\y= 3\mu`

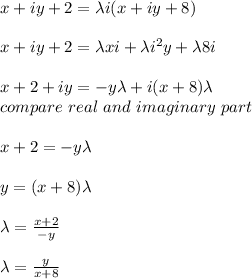
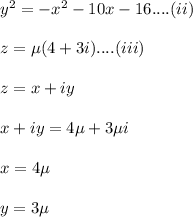
put the value of x, y in equation (ii) we get:

`5\mu +4=0\\\\\mu = (-4)/(5) \\\\`

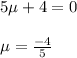
to put the of
`\mu` in equation (iii) we get:

`z= (-4)/(5) (4+3i) \\\\ \boxed{z= (-16)/(5)- (-12)/(15)i} \\`