Answer:
Explicit formula for the sequence is
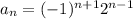
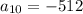
Explanation:
Given: Sequence is
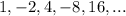
To find: explicit formula for the sequence and the
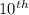 term of the sequence
term of the sequence
Solution:
A sequence is an ordered list of numbers which repetitions are allowed and order does matter.
![a_1=(-1)^(1+1)\left [ 2^((1-1)) \right ]=1\\a_2=(-1)^(2+1)\left [ 2^((2-1)) \right ]=-2\\a_3=(-1)^(3+1)\left [ 2^((3-1)) \right ]=4\\a_4=(-1)^(4+1)\left [ 2^((4-1)) \right ]=-8\\a_5=(-1)^(5+1)\left [ 2^((5-1)) \right ]=16](https://img.qammunity.org/2021/formulas/mathematics/college/thilp8usce5k66ipn3xk30k1xpu2hs6yde.png)
So, explicit formula for the sequence is
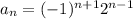
To find the
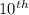 term of the sequence, put n = 10
term of the sequence, put n = 10
![a_(10)=(-1)^(10+1)\left [ 2^((10-1)) \right ]\\=(-1)^(11)2^9\\=-1(2^9)\\=-512](https://img.qammunity.org/2021/formulas/mathematics/college/1tubifzwcikb125qx4s1bdc67lcmkem974.png)