Question

Write the explicit formula for each sequence and use it to find the 10'' term of the sequence.

1,-2.4,-8.16,....​

Answer 1

Explicit formula for the sequence is
`a_n=(-1)^(n+1)2^(n-1)`

`a_(10)=-512`

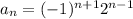
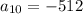
Explanation:

Given: Sequence is
`1,-2,4,-8,16,...`

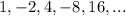
To find: explicit formula for the sequence and the
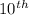`10^(th)` term of the sequence

Solution:

A sequence is an ordered list of numbers which repetitions are allowed and order does matter.

`a_1=(-1)^(1+1)\left [ 2^((1-1)) \right ]=1\\a_2=(-1)^(2+1)\left [ 2^((2-1)) \right ]=-2\\a_3=(-1)^(3+1)\left [ 2^((3-1)) \right ]=4\\a_4=(-1)^(4+1)\left [ 2^((4-1)) \right ]=-8\\a_5=(-1)^(5+1)\left [ 2^((5-1)) \right ]=16`

So, explicit formula for the sequence is
`a_n=(-1)^(n+1)2^(n-1)`

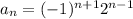
To find the
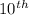`10^(th)` term of the sequence, put n = 10

`a_(10)=(-1)^(10+1)\left [ 2^((10-1)) \right ]\\=(-1)^(11)2^9\\=-1(2^9)\\=-512`