Question

You are designing a geartrain with three spur gears: one input gear, one idler gear,and one output gear. The diametral pitch for the geartrain is 16. The diameter of the input gear needs to be twice the diameter of the idler gear and three times the diameter of the output gear. The entire geartrain needs to fit into a rectangular footprint of no larger than 22 in. high and 15 in. long. Determine an appropriate number of teeth of the smallest gear.

Answer 1

The appropriate number of teeth of the smallest gear should is 58 teeth.

Step-by-step explanation:

The given parameters include;

The diametral pitch = 16

Number of gears = 3

Diameter of the input gear = 2 × diameter of the idler gear

Diameter of the input gear = 3 × diameter of the output gear

Height of footprint = 22 in.

Length of footprint = 15 in.

Let the size of the output gear = X

Therefore, the input gear = 3·X

The diameter of the idle gear = 2·X

Therefore, total width of the gear train = X + 2·X + 3·X = 6·X

Where 6·X = 22, X = 22/6 = 11/3 in.

Since the diametral pitch = 16 then we have;

`Diametral \, Pitch = (Number \, of \, teeth)/(Pitch \, diameter)`

`\therefore Diametral \, Pitch \, of \, the \, smallest \, gear =16 =(Number \, of \, teeth \, of \, the \, smallest \, gear)/((11)/(3) )`

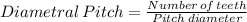
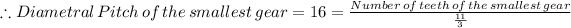
Hence, number of teeth of the smallest gear = 16 × 11/3 = 176/3 =
`58\tfrac{2}{3}`

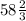
The appropriate number of teeth of the smallest gear should be 58

From which we have the diameter of the smallest gear = 58/16 = 3.625

The diameter of the input gear is then 3 × 3.625 = 10.875 in.

The diameter of the idler = 2 × 3.625 = 7.25 in.

The appropriate number of teeth of the smallest gear should = 58 teeth.