Answer:
v_avg = 37 km/h
Step-by-step explanation:
To find the average velocity in the complete trajectory you use the following formula:
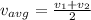 ( 1 )
( 1 )
v1: velocity in the first part of the trajectory = 70 km/h
v2: velocity in the second part of the trajectory = ?
You calculate v2 by using the following equation for a motion with constant velocity:
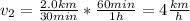
you replace the values of v1 and v2 in (1) and you obtain:
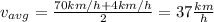
hence, the average velocity is 37 km/h