Answer:
Angle between the forces
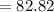 degrees
degrees
Step-by-step explanation:
The resultant force value
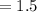 times of Force F
times of Force F
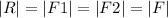
Where R is the resultant force
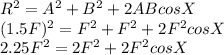
Cos X is the angle between the two forces.
On further simplifying the equation we get
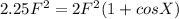
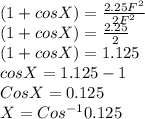
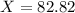 degrees
degrees
Angle between the forces
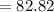 degrees
degrees