Question

Two equal forces F have resultant of 1.5F .Find the angle between the forces​

Answer 1

Angle between the forces​
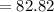`= 82.82` degrees

Step-by-step explanation:

The resultant force value
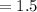`= 1.5` times of Force F

`|R| = |F1| = |F2| =|F|`

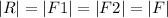
Where R is the resultant force

`R^2 = A^2 + B^2 + 2AB cos X\\(1.5F)^2 = F^2 + F^2 + 2F^2 cos X\\2.25F^2 = 2F^2 + 2F^2 cos X\\`

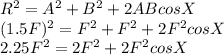
Cos X is the angle between the two forces.

On further simplifying the equation we get

`2.25F^2 = 2F^2(1 + cos X)`

`(1 + cos X) = (2.25F^2)/(2F^2) \\(1 + cos X) = (2.25)/(2) \\(1 + cos X) = 1.125\\cos X = 1.125 - 1\\Cos X = 0.125\\X = Cos^(-1)0.125\\`

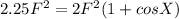
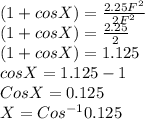
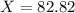`X = 82.82` degrees

Angle between the forces​
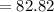`= 82.82` degrees