Write the equation of the directrix of the parabola shown below. Write your answer without using spaces. y^2 - 4x + 4y - 4= 0

Question

asked Dec 24, 2021 147k views

2 Answers

Gtournie · Answer 1 · 2021-12-31T05:29:10+0000

Answer:

y = - 3

Explanation:

The general form of the equation of a parabola is given by:

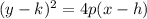
(y-k)^2=4p(x-h)

with foci (h,k) and directrix equation given by y = k - p.

The parabola equation that you have is

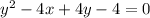
y^2-4x+4y-4=0

you complete squares to get the general form of the equation:

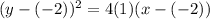
$(y^2+4y+4)-4-4=4x\\\\(y+2)^2=4x+8\\\\(y+2)^2=4(x-(-(8)/(4)))\\\\(y+2)^2=4(1)(x-(-2))$

(y-(-2))^2=4(1)(x-(-2))

Next, you compare the last expression with the general for of the equation of a parabola and you obtain:

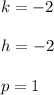
$k = -2\\\\h=-2\\\\p=1$

hence, the directrix equation is y = k - p = - 2 - 1 = - 3