Answer:
the tension in the wire =

Step-by-step explanation:
Parameters given include:
The height of the large tank = 1 m
Diameter D = 0.75 m
diameter of the nozzle where the water exit d = 15 mm = 0.015 m
The flow speed at the exit of the tank
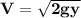
The first diagram shown in the attached file depicts and illustrate the sketch of the large tank that is fixed on the cart.
Now; using the x component of the momentum equation from the diagram; we have;
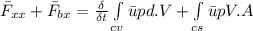
For steady flow:
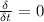
So:
T = u{║ρV₁A₁║}
T = ρV₁²A₁
where:
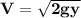
T =ρgy

replacing y= 0.9 m
The tension of the wire is:
T = 999 × 9.81 × 0.9 ×
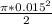
T =

Hence, the tension in the wire =

The schematic graphical representation showing the plot of the tension in the wire as a function of water depth for: 0 < y < 0.9 can be found in the document file attached below.