Explanation:
Let,
- x = Kevin's age
- y = Kevin's mother's age
Given that,
Kevin's age + Mother's age = 61
x + y = 61
 required equation for a)
required equation for a)

Now, we have two equations.
y - 3x = 1 -------(1)
y + x = 61 --------(2)
On solving them (using the substitution method),
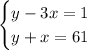
Take ----(1)
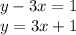
Now, substitute the value of y in ----(2)
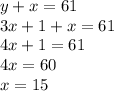
Substitute the value of x in -----(1),
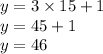
So,
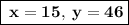
Now, by graphing them (see the attachment), the point of intersection is O (15, 46). Hence, from this we can infer that, Kevin is 15 years old while his mother is 46 years old.
 answer for b)
answer for b)
