Question

What value added to the set below would give a mean of 33?

{19, 27, 64, 36}
19

30

27

42

Answer 1

Answer is 19

If you add all of the numbers together including 19. You would get 165, then divide the total by 5. Your answer would be 33!

Answer 2

19

Explanation:

Given:

• data = [19,27,64,36]

• mean value = 33

To find:

• another data / last data

Therefore:

• New data is 19,27,64,36,x
• Where x is an unknown value/data.

Mean Value:

`\displaystyle \large{m=(1)/(n)\sum_(i =1)^n x_i \to (x_1+x_2+x_3+...+x_n)/(n)}`

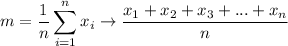
• m = mean value
• x1+x2+x3+...+xn = sum of all data
• n = amount of data

Therefore:

`\displaystyle \large{33=(19+27+64+36+x)/(5)}`

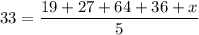
Solve for x - first, multiply both sides by 5 to clear out the denominator:

`\displaystyle \large{33\cdot 5=(19+27+64+36+x)/(5) \cdot 5}\\\displaystyle \large{165=19+27+64+36+x}`

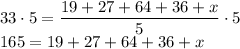
Evaluate the sum:

`\displaystyle \large{165=146+x}`

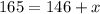
Subtract both sides by 146:

`\displaystyle \large{165-146=146-146+x}\\\displaystyle \large{19=x}`

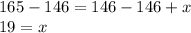
Therefore, another value/data that will give a mean value of 33 is 19.