Answer:
StartFraction StartRoot 30 EndRoot minus 3 StartRoot 2 EndRoot + StartRoot 55 EndRoot minus StartRoot 33 EndRoot Over 2
Explanation:
Given the surdic equation as shown
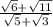
To find the quotient, we will rationalize by multipying both numerator and denominator of the function by the conjugate of the denominator.
Given the denominator
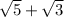 , its conjugate will be
, its conjugate will be

Multiplying through by
 , we have;
, we have;
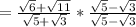
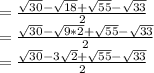
The final expression gives the requires answer