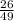Question

Forty-nine same-sized chips numbered from 1 to 49 are placed in a barrel. One chip is randomly pulled from the barrel. What is the probability that the number on the chip is greater than or equal to 24?

Answer 1

The probability that the number on the chip is greater than or equal to 24 is 0.531 or
`(26)/(49)`

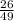
Explanation:

Given

Same Sized Chips

Number of Chips = 49

Required

The probability that the number on the chip is greater than or equal to 24

Given that all 49 chips are same sized, the means that they have equal probabilities;

Let C represent the event;

Hence,
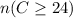`n(C\geq 24)` represents the chips numbered 24 and above

We're to calculate
`P(C\geq 24)` which represents the probability of obtaining a chip numbered 24 and above

`P(C\geq 24) = (n(C\geq 24))/(Total-chips)`

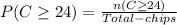
Chips numbered 24 and above are 24, 25, 26......49 and they're 26 in total

So,
`n(C\geq 24) = 26 chips`

`P(C\geq 24) = (n(C\geq 24))/(Total-chips)`

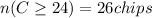
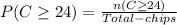
becomes

`P(C\geq 24) = (26)/(49)`

`P(C\geq 24) = 0.5306122449`

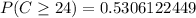
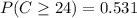`P(C\geq 24) = 0.531` -- approximated

Hence, the probability that the number on the chip is greater than or equal to 24 is 0.531 or
`(26)/(49)`