Answer: The determinant must be zero.
Explanation:
For a quadratic equation
a*x^2 + b*x + c = 0
The discriminant is:
D = b^2 - 4*a*c
and the solutions can be finded as:
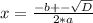
If D > 0 we have two real solutions
if D = 0 we only have one solution, x = -b/2a
If D < 0 we will have comples solutions, as we will have a negative number inside a square root.
Knowing that for this equation we have only one solution, then we can know that the determinant must be equal to zero.