Answer:
12 meters.
Explanation:
Given the height function of the rocket:
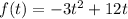
The function is a parabola which opens up and the maximum height is reached at the axis of symmetry.
Step 1: Determine the equation of symmetry
For any quadratic equation of the form
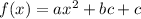 , the equation of symmetry is:
, the equation of symmetry is:
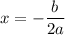 .
.
In the given function: a=-3, b=12
Equation of symmetry :
 .
.
Step 2: Substitute t=2 into f(t) to solve for the maximum height
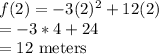
The maximum height reached by the rocket is 12 meters.