Question

The height in meters, of a model rocket above the ground is modeled by the function f (t) = -3t^2 + 12t, where t is time in seconds. What is the maximum height the rocket reaches

Answer 1

12 meters.

Explanation:

Given the height function of the rocket:
`f (t) = -3t^2 + 12t`

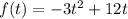
The function is a parabola which opens up and the maximum height is reached at the axis of symmetry.

Step 1: Determine the equation of symmetry

For any quadratic equation of the form
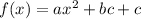`f(x)=ax^2+bc+c`, the equation of symmetry is:
`x=-(b)/(2a)`.

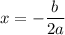In the given function: a=-3, b=12

Equation of symmetry :

`t=-(12)/(2*-3)\\t=2`.

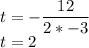Step 2: Substitute t=2 into f(t) to solve for the maximum height

`f (2) = -3(2)^2 + 12(2)\\=-3*4+24\\=12$ meters`

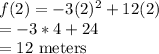
The maximum height reached by the rocket is 12 meters.