Question

Dilate line f by a scale factor of 2 with the center of dilation at the origin to create line f'. Where are points A' and B' located after dilation, and how are lines f and f' related?

The locations of A' and B' are A' (0, 4) and B' (4, 0); lines f and f' are parallel.
The locations of A' and B' are A' (0, 2) and B' (2, 0); lines f and f' are the same line.
The locations of A' and B' are A' (0, 2) and B' (4, 0); lines f and f' intersect at point A.
The locations of A' and B' are A' (0, 4) and B' (2, 0); lines f and f' intersect at point B

Answer 1

The locations of A' and B' are A' (0, 4) and B' (4, 0); lines f and f' are parallel.

Explanation:

Answer 2

Option (1).

Explanation:

Given question is incomplete: find the complete question in the attachment.

From the given figure, coordinates of the points A and B are (0, 2) and (2, 0) respectively.

Slope of line AB =
`((y_(2)-y_(1)))/((x_(2)-x_(1)))`

`m_(1)=(2-0)/(0-2)=-1`

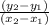
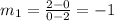
When these points are dilated by a scale factor = 2, about the origin

Rule for the dilation → (x, y) → (kx, ky)

Where k = scale factor

Coordinates of the points A' and B' will be (0, 4) and (4, 0)

Slope of the line A'B' =
`((y_(2)-y_(1)))/((x_(2)-x_(1)))`

`m_(2)=(4-0)/(0-4)=-1`

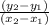
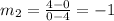
Since
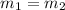`m_(1)=m_(2)` , both the lines AB and A'B' will be parallel.

Therefore, option (1) will be the answer.