Question

Under conditions for which the same room temperature is maintained by a heating or cooling system, it is not uncommon for a person to feel chilled in the winter but comfortable in the summer.

1. Provide a plausible explanation for this situation (with supporting calculations) by considering a room whose air temperature is maintained at 20°C throughout the year, while the walls of the room are nominally at 27°C and 14°C in the summer and winter, respectively. The exposed surface of a person in the room may be assumed to be at a temperature of 32°C throughout the year and to have an emissivity of 0.90. The coefficient associated with heat transfer by natural convection between the person and the room air is approximately 2W/m2*K.

Answer 1

summer case Q = 52.25 W/m²

winter case Q = 119.37 W/m²

Step-by-step explanation:

Given data

Air temperature T = 20 degree = 293 K

Environment temperature T1 = 27 degree = 300 K

Environment temperature T2 = 14 degree = 287 K

Surface temperature Ts = 32 degree = 305 K

Emissivity ε = 0.90

Coefficient of heat transfer h = 2 W/m²-K

Boltzman constant σ = 5.67 × 10-8 W/m²-
`k^4`

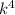
Solution:

We will apply here first Newton law for the and get here

q = h × A ( Ts – T) ……………………..1

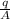`(q)/(A)` = 2 × (305 – 293)

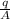`(q)/(A)` = 24 W/m²

Now we will apply here stefan Boltzam law for summer case

q = ε × A × σ ×
`( (Ts)^4- (T1)^4 )` ……………..2

put her value and we get

`(q)/(A) = 0.9 * 5.67 * 10^(-8) * ( (305)^4 - (300)^4 )`

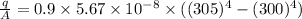
Solve it and we get

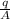`(q)/(A)` = 28.25 W/m²

Q = q(radiation) + q(convection) ……………….3

Q = 28.25 + 24

Q = 52.25 W/m²

And

For winter it will be

q = ε × A × σ ×
`( (Ts)^4 - (T2)^4 )` ……………..4

put her value and we get

`(q)/(A) = 0.9 * 5.67 * 10^(-8) * ( (305)^4 - (287)^4 )`

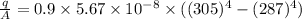
Solve it and we get

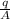`(q)/(A)` = 95.37 W/m²

Now put value in equation 3

Q = 95.37 + 24

Q = 119.37 W/m²

As we can say that here difference between the summer and winter time radiations flux and chilled conditions are attributes the effect of colder wall on radiations