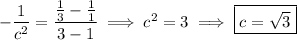Question

Verify that the function satisfies the hypotheses of the Mean Value Theorem on the given interval Then find all numbers c that satisfy the conclusion of the Mean Value Theorem: f(x) = 1/x on [1,3]​

Answer 1

f(x) = 1/x and its derivative f '(x) = -1/x² are discontinuous only at x = 0; everywhere else it is defined and behaves nicely in the sense that f is

• continuous on the closed interval [1, 3], and

• differentiable on the open interval (1, 3)

and the MVT holds.

The theorem says there is some real number c between 1 and 3 such that

`f'(c) = (f(3) - f(1))/(3 - 1)`

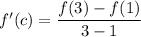
Solve for this c :

`-\frac1{c^2} = (\frac13-\frac11)/(3 - 1) \implies c^2 = 3 \implies \boxed{c = \sqrt3}`