Final answer:
The length of the diameter is 12.81 units.
Step-by-step explanation:
The length of a diameter in a circle can be found using the distance formula. By plugging in the coordinates of the two endpoints of the diameter (-5,4) and (3,-6) into the distance formula, we can calculate the distance between them. The formula for the distance between two points (x1, y1) and (x2, y2) is:
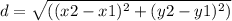
Plugging in the values, we get:
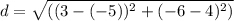
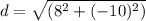
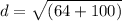
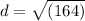
d = 12.81