Answer:
The difference between the average speed is 12 kilometers per hour, where Serah's train has the greatest speed.
Explanation:
Givens
- Javier's train travels 130 km in 75 minutes.
- Serah's train travels 377 km from 9:35 to 12:50.
The average speed is defined as
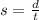
To finde Javier's speed, we need to transform 75 minutes into hours, we know that 1 hour is equivalent to 60 minutes.
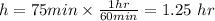
Now, we find the average speed
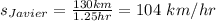
Therefore, Javier's train travels 104 kilometers per hour.
On the other hand, Serah's traing travels from 9:35 to 12:50, which is equivalent to 3 hours and 15 minutes, but 15 minutes is equivalent to 0.25, so the total time is 3.25 hours, so the average speed is
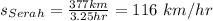
So, the difference would be
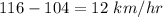
Therefore, the difference between the average speed is 12 kilometers per hour, where Serah's train has the greatest speed.