Question

PLEASE HELP

A bookshelf holds 6 different biographies and 4 different mystery novels. How many ways can one book of each type be selected?
11
30
24
20

Answer 1

There are 24 ways to select one book of each type.

Explanation:

In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.

The formula to compute the combinations of k items from n is given by the formula:

`{n\choose k}=(n!)/(k!(n-k)!)`

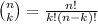
It is provided that there are 6 different biographies and 4 different mystery novels on a bookshelf.

Compute the number of ways to select a biography as follows:

Number of ways to select a biography =

`={6\choose 1}\\\\=(6!)/(1!(6-1)!)\\\\=(6* 5!)/(1* 5!)\\\\=6`

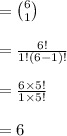
There are 6 ways to select a biography.

Compute the number of ways to select a mystery novel as follows:

Number of ways to select a mystery novel =

`={4\choose 1}\\\\=(4!)/(1!(4-1)!)\\\\=(4* 3!)/(1* 3!)\\\\=4`

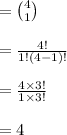
There are 4 ways to select a mystery novel.

Then the total number of way to select one book of each type is:

`{6\choose 1}* {4\choose 1}=6* 4=24`

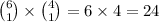
Thus, there are 24 ways to select one book of each type.