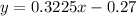Question

The accompanying data on x = current density (mA/cm2) and y = rate of deposition (m/min)μ appeared in a recent study.

x 20 40 60 80
y 0.24 1.20 1.71 2.22
a. Do you agree with the claim by the article’s author that "a linear relationship was obtained from the tin-lead rate of deposition as a function of current density"? (Hint: determine the coefficient of correlation and determination factors)
b. Determine the linear regression equation.

Answer 1

a)
`r=(4(333)-(200)(5.37))/(√([4(12000) -(200)^2][4(9.3501) -(5.37)^2]))=0.9857`

The correlation coefficient for this case is very near to 1 so then we can ensure that we have linear correlation between the two variables

b)
`m=(64.5)/(2000)=0.03225`

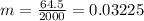
Now we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(200)/(4)=50`

`\bar y= (\sum y_i)/(n)=(5.37)/(4)=1.3425`

`b=\bar y -m \bar x=1.3425-(0.03225*50)=-0.27`

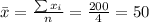
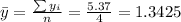
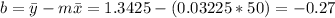
So the line would be given by:

`y=0.3225 x -0.27`

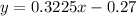
Explanation:

Part a

The correlation coeffcient is given by this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

For our case we have this:

n=4
`\sum x = 200, \sum y = 5.37, \sum xy = 333, \sum x^2 =12000, \sum y^2 =9.3501`

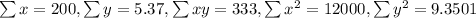
`r=(4(333)-(200)(5.37))/(√([4(12000) -(200)^2][4(9.3501) -(5.37)^2]))=0.9857`

The correlation coefficient for this case is very near to 1 so then we can ensure that we have linear correlation between the two variables

Part b

`m=(S_(xy))/(S_(xx))`

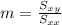
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

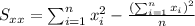
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=12000-(200^2)/(4)=2000`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i){n}}=333-(200*5.37)/(4)=64.5`

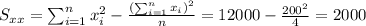
And the slope would be:

`m=(64.5)/(2000)=0.03225`

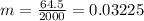
Now we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(200)/(4)=50`

`\bar y= (\sum y_i)/(n)=(5.37)/(4)=1.3425`

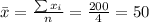
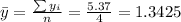
And we can find the intercept using this:

`b=\bar y -m \bar x=1.3425-(0.03225*50)=-0.27`

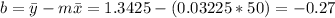
So the line would be given by:

`y=0.3225 x -0.27`