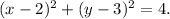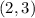Question

Write the equation of the circle graphed below.

Answer 1

As shown in picture, this circle has radius 1.5 and passes (0, 1.5)

=> According to the general form of equation of circle that has radius r and passes (a, b): (x - a)^2 + (y - b)^2 = r^2, we have:

x^2 + (y - 1.5)^2 = 1.5^2

<=>

x^2 + (y - 1.5)^2 = 2.25

Hope this helps!

:)

Answer 2

the equation of the circle is
`\( (x - 2)^2 + (y - 3)^2 = 4 \).`
`\( (2, 3) \)`

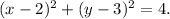
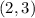
The equation of a circle in standard form is
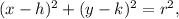`\( (x - h)^2 + (y - k)^2 = r^2 \),`where
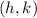`\( (h, k) \)` is the center of the circle and
`\( r \)` is the radius.

From the provided coordinates (0,3) and (4,3), we can deduce that:

1. The center of the circle is at the midpoint of the line segment joining these two points. Since the y-coordinate is the same (3) and the x-coordinates are 0 and 4, the midpoint is . This is the point
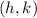`\( (h, k) \)` in the circle's equation.

2. The radius of the circle is the distance from the center to either of the points. Since both points have a y-coordinate of 3, we can simply take the difference in x-coordinates to find the radius. The radius
`\( r \)` is
`\( 4 - 2 = 2 \)`.

Now we can write the equation of the circle:

`\[ (x - 2)^2 + (y - 3)^2 = 2^2 \]`

`\[ (x - 2)^2 + (y - 3)^2 = 4 \]`

So the equation of the circle is
`\( (x - 2)^2 + (y - 3)^2 = 4 \).`
`\( (2, 3) \)`