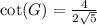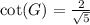Question

Right △EFG has its right angle at F, EG=6, and FG=4.

What is the value of the trigonometric ratio of an angle of the triangle?

Drag a value to each box to match the trigonometric ratio with its value.
cscE
cosG
cotG

Answer 1

Please find the attachment.

We have been given that △EFG has a right angle at F, EG=6, and FG=4. We are asked to find trigonometric ratio for given angles of the triangle.

First of all, we will draw a right triangle using our given information.

Now we will find length of side EF using Pythagoras theorem.

`EF^2=EG^2-FG^2`

`EF^2=6^2-4^2`

`EF^2=36-16`

`EF^2=20`

`EF=√(20)=2√(5)`

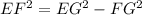
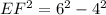
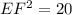
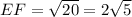
We know that cosecant relates hypotenuse with opposite side of right triangle.

`\csc=\frac{\text{Hypotenuse}}{\text{Opposite}}`

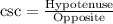
We can see that opposite side to angle E is FG and hypotenuse is EG.

`\csc(E)=(6)/(4)`

`\csc(E)=(3)/(2)`

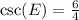
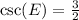
We know that cosine relates adjacent side with hypotenuse.

`\cos=\frac{\text{Adjacent}}{\text{Hypotenuse}}`

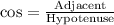
We can see that adjacent side to angle G is FG and hypotenuse is EG.

`\cos(G)=(4)/(6)`

`\cos(G)=(2)/(3)`

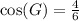
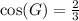
We know that cotangent relates adjacent side with opposite side of right triangle.

`\cot=\frac{\text{Adjacent}}{\text{Opposite}}`

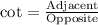
We can see that adjacent side to angle G is FG and opposite side is EG.

`\cot(G)=(4)/(2√(5))`

`\cot(G)=(2)/(√(5))`