We have been given that a tree that measured
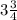 feet tall was planted. A hundred years later, the tree is now
feet tall was planted. A hundred years later, the tree is now
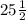 feet tall. We are asked to find the number of times times is tree now taller than it was when the school first opened.
feet tall. We are asked to find the number of times times is tree now taller than it was when the school first opened.
To solve our given problem, we will divide present length of tree by length of tree when it was planted as:
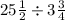
First of all we will convert mixed fractions into improper fractions.
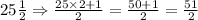
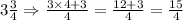
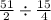
Now we will convert our division problem into multiplication problem by flipping the 2nd fraction as:

Cancel out common factors:
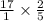

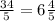
Therefore, the tree is
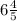 is taller now than it was when the school first opened and option A is the correct choice.
is taller now than it was when the school first opened and option A is the correct choice.