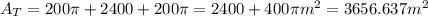Answer:
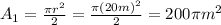
For the rectangular shape we have:
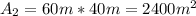

And the total area would be:
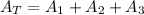
Replacing we got:
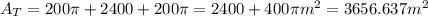
Explanation:
For this case using the figure attached we can separate the total area in 3 parts.
For this case
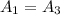 and represent the area for a semicircle and the A2 represent the area for a rectangular figure.
and represent the area for a semicircle and the A2 represent the area for a rectangular figure.
We can find the individual areas like this:
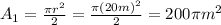
For the rectangular shape we have:
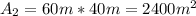

And the total area would be:
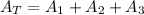
Replacing we got: