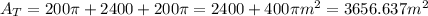Question

3. How many square meters are enclosed in
the track?

Answer 1

`A_1 = (\pi r^2)/(2) = (\pi (20m)^2)/(2)= 200 \pi m^2`

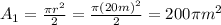
For the rectangular shape we have:

`A_2= 60 m* 40 m= 2400 m^2`

`A_3 = (\pi r^2)/(2) = (\pi (20m)^2)/(2)= 200 \pi m^2`

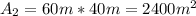
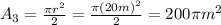
And the total area would be:

`A_T = A_1 +A_2 +A_3`

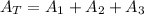
Replacing we got:

`A_T = 200 \pi +2400 +200 \pi = 2400 +400 \pi m^2= 3656.637 m^2`

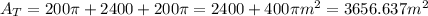
Explanation:

For this case using the figure attached we can separate the total area in 3 parts.

For this case
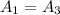`A_1 = A_3` and represent the area for a semicircle and the A2 represent the area for a rectangular figure.

We can find the individual areas like this:

`A_1 = (\pi r^2)/(2) = (\pi (20m)^2)/(2)= 200 \pi m^2`

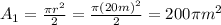
For the rectangular shape we have:

`A_2= 60 m* 40 m= 2400 m^2`

`A_3 = (\pi r^2)/(2) = (\pi (20m)^2)/(2)= 200 \pi m^2`

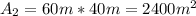
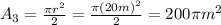
And the total area would be:

`A_T = A_1 +A_2 +A_3`

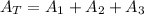
Replacing we got:

`A_T = 200 \pi +2400 +200 \pi = 2400 +400 \pi m^2= 3656.637 m^2`