Question

Exhaust gas from a furnace is used to preheat the combustion air supplied to the furnace burners. The gas, which has a flow rate of 15 kg/s and an inlet temperature of 1100 K, passes through a bundle of tubes, while the air, which has a flow rate of 10 kg/s and an inlet temperature of 300 K, is in cross flow over the tubes. The tubes are unfinned, and the overall heat transfer coefficient is 90 W/m2·K.

Determine the total tube surface area, in m2, required to achieve an air outlet temperature of 850 K. The exhaust gas and the air may each be assumed to have a specific heat of 1075 J/kg·K.

Answer 1

The total tube surface area in m² required to achieve an air outlet temperature of 850 K is 192.3 m²

Step-by-step explanation:

Here we have the heat Q given as follows;

Q = 15 × 1075 × (1100 -
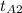`t_(A2)`) = 10 × 1075 × (850 - 300) = 5912500 J

∴ 1100 -
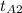`t_(A2)` = 1100/3

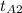`t_(A2)` = 733.33 K

`\Delta \bar{t}_(a) =\frac{t_{A_(1)}+t_{A_(2)}}{2} - \frac{t_{B_(1)}+t_{B_(2)}}{2}`

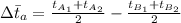
Where

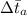`\Delta \bar{t}_(a)` = Arithmetic mean temperature difference

`t_{A_(1)` = Inlet temperature of the gas = 1100 K

`t_{A_(2)` = Outlet temperature of the gas = 733.33 K

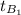`t_{B_(1)` = Inlet temperature of the air = 300 K

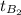`t_{B_(2)` = Outlet temperature of the air = 850 K

Hence, plugging in the values, we have;

`\Delta \bar{t}_(a) =(1100+733.33)/(2) - (300+850)/(2) = 341\tfrac{2}{3} \, K = 341.67 \, K`

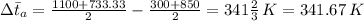
Hence, from;

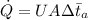`\dot{Q} = UA\Delta \bar{t}_(a)`, we have

5912500 = 90 × A × 341.67

`A = (5912500 )/(90 * 341.67) = 192.3 \, m^2`

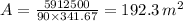
Hence, the total tube surface area in m² required to achieve an air outlet temperature of 850 K = 192.3 m².