Answer:
The total tube surface area in m² required to achieve an air outlet temperature of 850 K is 192.3 m²
Step-by-step explanation:
Here we have the heat Q given as follows;
Q = 15 × 1075 × (1100 -
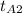 ) = 10 × 1075 × (850 - 300) = 5912500 J
) = 10 × 1075 × (850 - 300) = 5912500 J
∴ 1100 -
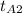 = 1100/3
= 1100/3
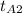 = 733.33 K
= 733.33 K
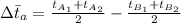
Where
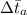 = Arithmetic mean temperature difference
= Arithmetic mean temperature difference
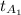 = Inlet temperature of the gas = 1100 K
= Inlet temperature of the gas = 1100 K
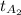 = Outlet temperature of the gas = 733.33 K
= Outlet temperature of the gas = 733.33 K
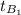 = Inlet temperature of the air = 300 K
= Inlet temperature of the air = 300 K
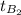 = Outlet temperature of the air = 850 K
= Outlet temperature of the air = 850 K
Hence, plugging in the values, we have;
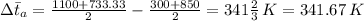
Hence, from;
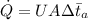 , we have
, we have
5912500 = 90 × A × 341.67
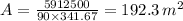
Hence, the total tube surface area in m² required to achieve an air outlet temperature of 850 K = 192.3 m².