1. For the first inequality, Luz can buy less than 5 computers (since
 represents the number of computers and must be less than 5).
represents the number of computers and must be less than 5).
2. For the second set of inequalities,
 must be greater than -6 and less than 0.
must be greater than -6 and less than 0.
The image shows a mathematical problem with two inequalities:
1.

2.
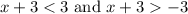
To solve these inequalities step by step, we'll perform the following calculations:
For the first inequality:
![\[ 70x < 350 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/vxpr19e7auu9gavldn484f5hawfv2oi5pe.png)
1. Divide both sides by 70 to solve for x:
![\[ x < (350)/(70) \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jrcdbr1673ocqlzmrak8cm48y76da2aca2.png)
For the second set of inequalities:
![\[ x + 3 < 3 \] and \( x + 3 > -3 \)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/in23deyap2fpzfib71p96upustpq0mi0fi.png)
1. Subtract 3 from all parts of the compound inequality:
![\[ x < 3 - 3 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/y3tpxi9q21jt5b0frz7ehmudmqu9s8da0m.png) and
and
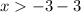
![\[ x < 0 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/2mwpkn51fl6h3txoq3789l2pwvixow75bp.png) and
and
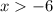
Now let's calculate the values.
Solution for the inequalities:
First inequality:
![\[ 70x < 350 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/vxpr19e7auu9gavldn484f5hawfv2oi5pe.png)
After dividing both sides by 70, we get:
![\[ x < 5 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/zeh204ssjpjooywe50fzgr55o59lcpi55z.png)
Second set of inequalities:
![\[ x + 3 < 3 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/l4e3p3boc2pypn7958r7q2vv48fvf3vmt0.png) and
and
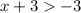
After subtracting 3 from all parts of the compound inequality, we get:
![\[ x < 0 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/2mwpkn51fl6h3txoq3789l2pwvixow75bp.png) and
and
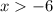
Thus, the solution to the inequalities are:
1. For the first inequality, Luz can buy less than 5 computers (since
 represents the number of computers and must be less than 5).
represents the number of computers and must be less than 5).
2. For the second set of inequalities,
 must be greater than -6 and less than 0.
must be greater than -6 and less than 0.
If we interpret
 as the number of items Luz can buy, the negative values don't make sense in a real-world context, as you cannot buy a negative number of items. Therefore, the practical solution for the second inequality is that Luz cannot buy any items since
as the number of items Luz can buy, the negative values don't make sense in a real-world context, as you cannot buy a negative number of items. Therefore, the practical solution for the second inequality is that Luz cannot buy any items since
 must be less than 0 and whole numbers (non-negative integers) are required for the count of items.
must be less than 0 and whole numbers (non-negative integers) are required for the count of items.