Question

Mr. auric goldfinger, criminal mastermind, intends to smuggle several tons of gold across international borders by disguising it as lumps of iron ore. he commands his engineer minions to form the gold into little spheres with a diameter of exactly and paint them black. however, his chief engineer points out that customs officials will surely notice the unusual weight of the "iron ore" if the balls are made of solid gold (density ). he suggests forming the gold into hollow balls instead (see sketch at right), so that the fake "iron ore" has the same density as real iron ore one of the balls of fake "iron ore," sliced in half. calculate the required thickness of the walls of each hollow lump of "iron ore." be sure your answer has a unit symbol, if necessary, and round it to significant digits.

Answer 1

The thickness of the walls of each hollow lump of "iron ore" is 2.2 cm

Step-by-step explanation:

Here we have that the density of solid gold = 19.3 g/cm³

Density of real iron ore = 5.15 g/cm³

Diameter of sphere of gold = 4 cm

Therefore, volume of sphere = 4/3·π·r³ = 4/3×π×2³ = 33.5 cm³

Mass of equivalent iron = Density of iron × Volume of iron = 5.15 × 33.5

Mass of equivalent iron = 172.6 cm³

∴ Mass of gold per lump = Mass of equivalent iron = 172.6 cm³

Volume of gold per lump = Mass of gold per lump/(Density of the gold)

Volume of gold per lump = 172.6/19.3 = 8.94 cm³

Since the gold is formed into hollow spheres, we have;

Let the radius of the hollow sphere = a

Therefore;

Total volume of the hollow gold sphere = Volume of gold per lump - void sphere of radius, a

Therefore;

`33.5 = 8.94 - (4)/(3) * \pi * a^3`

`(4)/(3) * \pi * a^3 = 33.5 - 8.94`

`a^3 = (24.6)/((3)/(4) \pi ) = 5.9`

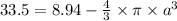
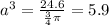
a = ∛5.9 = 1.8

The thickness of the walls of each hollow lump of "iron ore" = r - a = 4 - 1.8 = 2.2 cm.