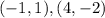Answer:
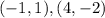
Explanation:
Given: The hypotenuse of a right triangle has endpoints A(4, 1) and B(–1, –2).
To find: coordinates of vertex of the right angle
Solution:
Let C be point
Distance between points
 is given by
is given by
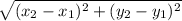
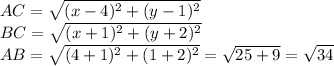
ΔABC is a right angled triangle, suing Pythagoras theorem (square of hypotenuse is equal to sum of squares of base and perpendicular)
![34=\left [ (x-4)^2+(y-1)^2 \right ]+\left [ (x+1)^2+(y+2)^2 \right ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/59p335f9xqq9e7j9yvsxs4d8cf7t6vdyar.png)
Put
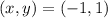
![34=\left [ (-1-4)^2+(1-1)^2 \right ]+\left [ (-1+1)^2+(1+2)^2 \right ]\\34=25+9\\34=34](https://img.qammunity.org/2021/formulas/mathematics/high-school/qr424yzfp1g735hyk3kij53btewu0wq1yo.png)
which is true. So,
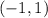 can be a vertex
can be a vertex
Put
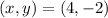
![34=\left [ (4-4)^2+(-2-1)^2 \right ]+\left [ (4+1)^2+(-2+2)^2 \right ]\\34=9+25\\34=34](https://img.qammunity.org/2021/formulas/mathematics/high-school/gtaqp1roprt0frxeuafne6nhk4ay3xfati.png)
which is true. So,
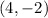 can be a vertex
can be a vertex
Put
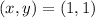
![34=\left [ (1-4)^2+(1-1)^2 \right ]+\left [ (1+1)^2+(1+2)^2 \right ]\\34=9+4+9\\34=22](https://img.qammunity.org/2021/formulas/mathematics/high-school/hw4y3y3c2wzwu7mdv30bn5zf1zedq4gz44.png)
which is not true. So,
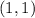 cannot be a vertex
cannot be a vertex
Put
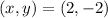
![34=\left [ (2-4)^2+(-2-1)^2 \right ]+\left [ (2+1)^2+(-2+2)^2 \right ]\\34=4+9+9\\34=22](https://img.qammunity.org/2021/formulas/mathematics/high-school/ey2qts2otrvcwprtkcv3zu8wtffmosk8i6.png)
which is not true. So,
 cannot be a vertex
cannot be a vertex
Put

![34=\left [ (4-4)^2+(-1-1)^2 \right ]+\left [ (4+1)^2+(-1+2)^2 \right ]\\34=4+25+1\\34=30](https://img.qammunity.org/2021/formulas/mathematics/high-school/grntvpy0e1dwmmhgp9eeeh84banvv0fhxm.png)
which is not true. So,
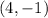 cannot be a vertex
cannot be a vertex
Put
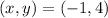
![34=\left [ (-1-4)^2+(4-1)^2 \right ]+\left [ (-1+1)^2+(4+2)^2 \right ]\\34=25+9+36\\34=70](https://img.qammunity.org/2021/formulas/mathematics/high-school/x3e5zznvf9x1emdo24614e391uu18r1qu4.png)
which is not true. So,
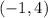 cannot be a vertex
cannot be a vertex
So, possible points for the vertex are