Question

Find the variance of the set of data to the nearest tenth: 5, 8, 2, 9, 4

Answer 1

Therefore the variance on the data set is 8.3

Explanation:

In order to find the variance of the set of data we first need to calculate the mean of the set, which is given by:

mean = sum of each element / number of elements

mean = (5 + 8 + 2 + 9 + 4)/5 = 5.6

We can now find the variance by applying the following formula:

`s^(2) = (\sum_((i=1))^n(x_i - mean)^2)/(n -1)`

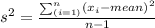
So applying the data from the problem we have:

s² = [(5 - 5.6)² + (8 - 5.6)² + (2 - 5.6)² + (9 - 5.6)² + (4 - 5.6)²]/(5 - 1)

s² = [(-0.6)² + (2.4)² + (-3.6)² + (3.4)² + (-1.6)²]/4

s² = [0.36 + 5.76 + 12.96 + 11.56 + 2.56]/4 = 8.3

Therefore the variance on the data set is 8.3