Answer:
13.8 metres ≈ 14 metres
Explanation:
Let's say the distance from the tree to point B is x. We need to use trigonometry for this problem - specifically tangent, which is opposite divided by adjacent.
Here, we're going to have two equations. One of them involves point B and the other involves point A. Let's do the point B one first:
tan(32) = h/x
Now, for the point A one, where the angle is 19, our opposite is still h, but our adjacent side is different; it's the distance from the tree to A, which includes the distance from the tree to B. That distance is x, but we need to add AB to it, so our adjacent side is x + 18. Then our equation is:
tan(19) = h/(x + 18)
We now have two equations and two variables. Let's take the first equation and solve it for x in terms of h because h is what we want to find:
tan(32) = h/x
x = h/tan(32)
Substitute this expression in for x in the second equation:
tan(19) = h/(x + 18)
tan(19) = h/[(h/tan(32)) + 18]
[h/tan(32) + 18] * tan(19) = h
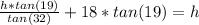
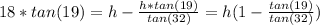
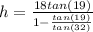 ≈ 13.8 metres
≈ 13.8 metres
The answer is 13.8 metres, or, if rounded to the nearest whole number, it is 14 metres.