Answer:
x = 4
which agrees with the third listed answer among the given options
Explanation:
We can re-write the logarithmic equation using the properties of logarithms:
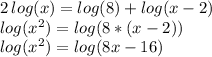
Therefore, the arguments of the log functions must also be equal (and we can solve for "x" by noticing that this expression is the perfect square of a binomial:
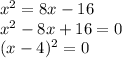
and for this equation to verify, x must be 4