Answer:
The correlation coefficient of the data is 0.8679.
Explanation:
The formula to compute the correlation coefficient is:
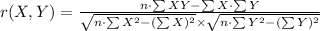
From the data provided compute the values of ∑ XY, ∑ X, ∑ Y, ∑ X² and ∑ Y².
The values are computed in the table below.
Compute the correlation coefficient as follows:
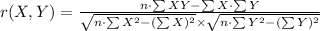

Thus, the correlation coefficient of the data is 0.8679.