Question

Could -free, automatic faucets actually be housing more bacteris than the old fashioned, manual kind The concern is that decreased water flow may increase the chance that bacteria grows, because the automatic faucets are not being thoroughly flushed through. It is known that 15% of cultures from older faucets in hospital patient care areas test positive for Legionella bacteria. A recent study at Johns Hopkins Hospital found Legionella bacteria growing in 10 of cultured water samples from 20 electronic faucets aIf the probability of Legionella bacteria growing in a faucet is 0.15, what is the prob ability that in a sample of 20 faucets. 10 or more have the bacteria growing (the Johns Hopkins study provide sufficient evidence that the probability of Legionella bacteria growing in electronic faucets is greater than 15%? Explain.

Answer 1

Not enough evidence to reject Null hypothesis

Explanation:

Solution:-

- A comparative study for bacterial growth in manual and electronic faucets is made.

- It is observed that there is a higher growth in electronic faucets due to slower flow rates, i.e electronic faucets are not thoroughly flushed; hence, giving more resident time for the scaled bacteria to grow.

- It is known that 15% of cultures from older faucets were tested positive for the Legionella bacteria.

- A study at John Hopkins was conducted on a sample n = 20 electronic faucets with the probability of bacteria growing in a faucet is 0.15.

- We will conduct a hypothesis for at-least half proportion of electronic faucets have cultured bacteria.

- State the hypothesis for the proportion of electronic faucets culturing Legionella bacteria:

Null Hypothesis: P = 0.15

Alternate hypothesis: P > 0.15

- To determine the test statistics for the study conducted at John hopkins. We had a sample size of n = 20, and the probability for a bacteria to grow in a faucet is 0.15.

- Denote random variable, X: The number of electronic faucets culturing Legionella bacteria.

- Since, the probability for a bacteria to grow in a faucet is independent for each new faucet. We will assume the RV " X " to follow binomial distribution with probability of success 0.15:

X ~ Bin ( 20 , 0.15 )

- We are to determine that at-least half of the sample is subjected to the said bacteria. This is the probability of P ( X ≥ 10 ).

- The pmf for a binomially distributed random variable X is given below:

`P ( X = r ) = n_C__r * ( p(success) )^r * ( p (fail) )^(^n^-^r^)`

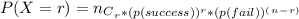
Where,

p ( success ) = 0.15

p ( fail ) = 1 - p ( success ) = 1 - 0.15 = 0.85

- Use the pmf to determine the required test statistics:

`P ( X \geq 10 ) = 1 - P ( X \leq 9 )\\\\P ( X \geq 10 ) = 1 - [ (0.85)^2^0 + 20*(0.15)*(0.85)^1^9 + 20_C_2 (0.15)^2*(0.85)^1^8 +\\\\ 20_C_3 (0.15)^3*(0.85)^1^7 + 20_C_4 (0.15)^4*(0.85)^1^6 + 20_C_5 (0.15)^5*(0.85)^1^5+\\\\ 20_C_6 (0.15)^6*(0.85)^1^4 + 20_C_7 (0.15)^7*(0.85)^1^3 + 20_C_8 (0.15)^8*(0.85)^1^2 + \\\\ 20_C_9 (0.15)^9*(0.85)^1^1\\\\\\P ( X \geq 10 ) = 1 - [ 0.03875 + 0.13679 + 0.22933 + 0.24282 + 0.18212 + 0.10284 + \\\\ 0.04537 + 0.01601 + 0.00459 + 0.00108 ]\\\\`

`P ( X \geq 10 ) = 1 - [ 0.997 ] = 0.003`

- The probability that 10 or more electronic faucets is found to have Legionella bacteria growing is 0.003

- The test proportion of 10 and more electronic faucets have culturing bacteria is p = 0.003.

- Assuming normality of the population, the Z-statistics would be:

`Z-test = ( (p - P) √(n) )/(√(P*(1 - P )) ) \\\\Z-test = ( (0.003 - 0.15) √(20) )/(√(0.15*(0.85)) ) \\\\Z-test = -1.84109`

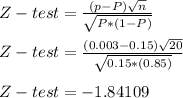
- If we were to test the claim to 90% level of confidence:

significance level (α) = 1 - CI = 1 - 0.9 = 0.1

- The rejection region Z-critical is defined by a right-tail:

`Z-critical \geq Z_\alpha \geq Z_0_._2\\\\Z-critical \geq 1.28`

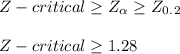
- Compare the test statistics with the rejection criteria defined by the Z-critical:

Z-test < Z-critical

-1.84 < 1.28

Conclusion:

There is not enough evidence that the probability of Legionella bacteria growing in electronic faucets is greater than 15%.